有哪些有趣而著名的悖论？

在数学中，有哪些非常有趣的悖论？

贝克莱悖论、罗素悖论、意料不到悖论、鳄鱼悖论、分球悖论等等。

悖论：指自相矛盾的命题，这个命题中隐含着两个对立的结论，而这两个结论都能自圆其说。（悖：混乱，相冲突；论：言论，言语。）

历史上出现过的数学悖论很多，数理逻辑是数学的研究方法，于是很多逻辑上的悖论，也归在数学门下，以下就是几个有趣的数学悖论：

贝克莱悖论

在17世纪，牛顿和莱布尼兹各自都独立创立了微积分，但是两人对微积分中“无穷小量”的定义不明确，导致了后来的第二次数学危机。

到了1734年，英国大主教贝克莱驳斥微积分理论（本质是反科学），指出了著名的贝克莱悖论，该悖论把当时微积分中最大缺陷暴露了出来：

关于第二次数学危机的解决，直到19世纪后，由众多数学家，比如波尔查、柯西、阿贝尔和康托尔等等，建立了更严密的数学定义后，才得到彻底解决。

罗素悖论

大名鼎鼎的罗素悖论（也称理发师悖论），直接导致了第三次数学危机的出现。

19世纪末，第二次数学危机在集合论的完善下得到解决，数学家们“欢欣起舞”。在1900年国际数学家大会上，法国大数学家庞加莱甚至宣称：现在的数学，已经达到了绝对严密的程度！

没想到三年之后，英国数学家、逻辑学家和哲学家——罗素，提出著名的理发师悖论，震惊了整个数学界：

罗素悖论的通俗解释：城市中的所有人，都在一位技艺高超的理发师那刮脸，这位理发师说到：“我只为本城市中，不给自己刮脸的人刮脸”！于是，其他人对理发师说：那么你给自己刮脸吗？

分析：倘若他不给自己刮脸，那么他属于“不给自己刮脸的人”，按照他的说法他就要给自己刮脸；倘若他给自己刮脸，他又属于“给自己刮脸的人”，按照他的说法就不该给自己刮脸。

罗素悖论的出现，说明集合论本身是不完备的；直到1908年，数学家建立起了公理化系统，才让集合论从根本上避免了罗素悖论。

预料不到悖论

一位学生会会长宣布：在下星期一到星期五的某一天下午开会，但是你们无法提前知道哪一天开会，因为只有到了当天早上的8点钟，我才会通知你们。

如果我们仔细分析这段话，会发现存在自相矛盾，使得开会无法进行，你能看出问题所在吗？

鳄鱼悖论

这是古希腊的一个故事：一条鳄鱼从一位母亲的手中夺走了孩子，母亲苦苦哀求说：求求你放过我的孩子，你提什么要求我都答应。

于是鳄鱼得意地说到：可以，那么你猜猜，我会不会吃掉你的孩子，如果你猜对了，我就把孩子还给你！

这位母亲细想片刻说到：我想你会吃掉我的孩子！

鳄鱼琢磨了一会愣住了，心想：我要是吃掉孩子，说明你猜对了，我应该把孩子还给你；如果我不吃掉你的孩子，说明你猜错了，我又要吃掉你的孩子！

分球悖论

悖论意指自相矛盾的命题，但是在一些数学悖论中，也指代某些数学命题，只是该命题与人们的常识相悖，比如分球悖论就是这样的。

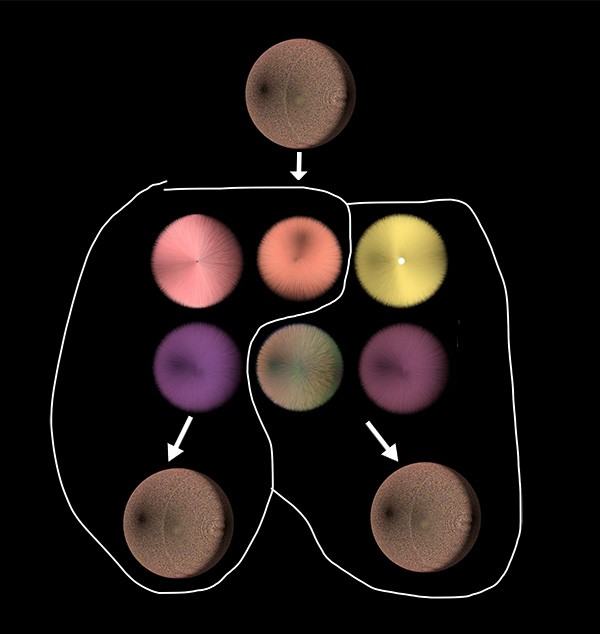
分球悖论，数学中一条经过严格证明的定理，可以描述为：一个三维实心球，必定存在一种办法分成有限部分，然后仅仅通过旋转和平移，就可以组成两个和原来完全相同的球（半径相同，密度相同……所有性质都相同）

科学上有哪些著名的悖论？

（1）黄油猫悖论：猫在半空中跳下，永远用脚着陆。把黄油吐司抛到半空中，永远是涂上‎黄油的一面落地。这个悖论出现在，你把黄油吐司没有涂上黄油的一面黏着猫的背部之时，让猫从半空中跳下。依照以上两条定律，猫无法用脚着陆，因为黄油吐司永远在涂上黄油的一面落地；但同样的，黄油吐司涂上黄油的一面无法落地，因为猫永远用脚着陆。

（2）生日悖论：如果一个房间里有23个或23个以上的人，那么至少有两个人的生日相同的概率要大于50%。这就意味着在一个典型的标准小学班级(30人)中，存在两人生日相同的可能性更高。对于60或者更多的人，这种概率要大于99%。这个数学事实与一般直觉相抵触，所以称得上是一个悖论。大多数人会认为，23人中有2人生日相同的概率应该远远小于50%。

（3）打官司悖论：有师徒二人，徒弟跟随师傅学习律师。收徒的时候，徒弟和师傅说好，毕业之后只要徒弟打赢了第一场官司，他就付学费，否则一分钱不给。

毕业之后，徒弟宣布以后再也不给学费，于是师傅一怒之下把徒弟告上法庭。开庭之前，徒弟对师傅说：“如果官司我赢了，那我肯定不用付钱；如果我输了，那当初说好了，我不能付学费。”

师傅反驳说：“如果你赢了，付钱是必须的；如果我赢了，那么根据法律判决，你也要付学费，自己看着办吧！”

（4）二分法悖论：运动是不可能的。你要到达终点，必须先到达全程的1/2处；要到达1/2处，必须先到1/4处……每当你想到达一个点，总有一个中点需要先到，因此你是永远也到不了终点的。

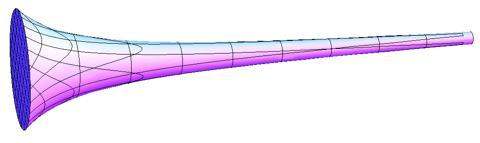
（5）几何悖论：17世纪的几何悖论。意大利数学家托里拆利将y=1/x中x≥1的部分绕着x轴旋转了一圈，得到了上面的小号状图形（注：下图只显示了一部分图形）。然后他得出：这个小号的表面积无穷大，可体积却是π。

（6）土豆悖论：100克土豆含有99%的水，如果它被榨出了2%，还剩98%的水分，它将只重50克。即100克的土豆含有1克干物质（drymaterial），当还剩98%的水分时，1克将对应2%的含量，因此含98%水分的土豆重50克。

求几个经典的悖论

（1）理发师悖论：1919年，罗素把他提出的集合论悖论通俗化如下：萨魏尔村有一位理发师，他给自己订下一条规则：他只给村子里自己不给自己刮胡子的人刮胡子。请问他该不该给自己刮胡子？

（2）苏格拉底悖论：苏格拉底有一句名言：“我只知道一件事，那就是什么都不知道。”

（3）纸牌悖论：纸牌悖论就是纸牌的一面写着：“纸牌反面的句子是对的。”而另一面却写着：“纸牌反面的句子是错的。”这是由英国数学家Jourdain提出来的。我们同样推不出结果来。

（4）上帝万能悖论：“如果说上帝是万能的，他能否创造一块他举不起来的大石头？”

（5）鳄鱼悖论：一条鳄鱼抢走了一个小孩，它对孩子的母亲说：“我会不会吃掉你的小孩？答对了，孩子还给你；答错了，我就吃了他。” 请问孩子母亲该如何回答才能保住孩子的性命

（6）老子悖论：“知者不言，言者不知。”是一条悖论，被白居易一语道穿。白居易在《读老子》里说道：“言者不知知者默，此语吾闻于老君。若道老君是知者，缘何自着五千文？”

扩展资料：

悖论是表面上同一命题或推理中隐含着两个对立的结论，而这两个结论都能自圆其说。悖论的抽象公式就是：如果事件A发生，则推导出非A，非A发生则推导出A。

悖论是命题或推理中隐含的思维的不同层次、意义（内容）和表达方式（形式）、主观和客观、主体和客体、事实和价值的混淆，是思维内容与思维形式、思维主体与思维客体、思维层次与思维对象的不对称，是思维结构、逻辑结构的不对称。悖论根源于知性认识、知性逻辑（传统逻辑）、矛盾逻辑的局限性。

产生悖论的根本原因是把传统逻辑形式化、把形式逻辑普适性绝对化，即把形式逻辑当做思维方式。所有悖论都是因形式逻辑思维方式产生，形式逻辑思维方式发现不了、解释不了、解决不了的逻辑错误。所谓解悖，就是运用对称逻辑思维方式发现、纠正悖论中的逻辑错误。

性质

悖论是命题或推理中隐含的思维的不同层次、意义（内容）和表达方式（形式）、主观和客观、主体和客体、事实和价值的混淆，是思维内容与思维形式、思维主体与思维客体、思维层次与思维对象的不对称，是思维结构、逻辑结构的不对称。

根源

悖论根源于知性认识、知性逻辑（传统逻辑）、矛盾逻辑的局限性。产生悖论的根本原因是把传统逻辑形式化、把传统逻辑普适性绝对化，即把形式逻辑当作思维方式。

用对称逻辑解“鳄鱼困境悖论”

一个鳄鱼偷了一个父亲的儿子，它保证如果这个父亲能猜出它要做什么，它就会将儿子还给父亲。如果这个父亲猜“鳄鱼不会将儿子还给他”，就会成为所谓的“悖论”：如果鳄鱼不还儿子，那么父亲就猜对了，鳄鱼就必须把孩子还给父亲，否则鳄鱼违背了诺言;如果鳄鱼将儿子还给他，那么父亲就猜错了，鳄鱼又违背了诺言。

解悖：鳄鱼“要做什么”是一种心理状态，鳄鱼“把孩子还给父亲”是一种行为，二者在时间上是前后衔接的两个阶段。同样，这个父亲猜“鳄鱼不会将儿子还给他”是鳄鱼心理状态，后来“鳄鱼将儿子还给他”是鳄鱼行为。

这个父亲猜“鳄鱼不会将儿子还给他”这种鳄鱼的心理状态和后来“鳄鱼将儿子还给他”这种鳄鱼行为之间同时存在并不矛盾——正是因为这个父亲猜对了鳄鱼的心理“不把儿子还给他”，所以鳄鱼为了履行诺言必须在行动上把儿子还给他。在这里对称逻辑通过限定时间范围，使语言的内容和语言的对象对称。

参考资料：百度百科-悖论

世界十大著名悖论

世界十大著名悖论分别是电车难题、空地上的奶牛、定时炸弹、爱因斯坦的光线、特修斯之船、伽利略的重力实验、猴子和打字机、中文房间、薛定谔的猫、缸中的大脑。

电车难题最早是由哲学家Philippa Foot提出的，用来批判伦理哲学中的主要理论，特别是功利主义。功利主义提出的观点是，大部分道德决策都是根据为最多的人提供最大的利益的原则做出的。

空地上的奶牛最初是被EdmundGettier用来批判主流上作为知识的定义的JTB（justifiedtrue belief）理论，即当人们相信一件事时，它就成为了知识。这件事在事实上是真的，并且人们有可以验证的理由相信它。

悖论简介

悖论，指在逻辑上可以推导出互相矛盾之结论，但表面上又能自圆其说的命题或理论体系。逻辑上的悖论震撼了逻辑和数学的基础，而伦理思想层面的悖论则可以激发人们深刻的思考。悖论是同一命题或推理中隐含着两个对立的结论，而这两个结论都能自圆其说。

悖论根源于知性认识、知性逻辑（传统逻辑）、矛盾逻辑的局限性。其都是因形式逻辑思维方式产生，形式逻辑思维方式发现、解释或解决不了的逻辑错误。

有名的悖论有哪些？

1、白马非马

说到悖论，绝对少不了的就是我国战国时期公孙龙的那条著名悖论：白马非马。公孙龙认为，白马并不是马，因为“马”强调的是一种生命，而“白马”强调的是一种颜色，二者的定义不同。

有人问公孙龙：如果现在有一匹白马，那么我们就不能说没有马。既然有白马就是有马的意思，为什么还说白马不是马呢？

公孙龙说：如果说想要找一匹马，那么即使是拉来一匹黄马或者黑马，都是可以的。如果你想要一匹白马，那么黄马或者黑马就不行了。如果说白马就是马，那么找一匹白马就等于找一匹马的意思。如果我说我要一匹白马，你却拉来一匹黄马或者黑马，这显然是不对的。由此可见，白马不是马。

又有人问：天底下的马都有各自的颜色，照你这么说，难道世界上就没有马了么？公孙龙又说：马本来就有颜色，所以才有白马。如果马没有颜色，只有它自己，又哪来的白马一说呢？所以，说到白就不是说马了，白马的要求是：既要是马还必须要是白色的，所以白马不是马。

后面还有很多双方讨论的问题，但限于篇幅我们就不赘言了，相信大家也从这一段里体会到了公孙龙大概的主旨。到了今天，仍然有很多人从逻辑学角度甚至是数学的角度来思考这个问题。

2、绞刑悖论

在著名的小说《堂·吉诃德》中，作者描述了一个非常奇怪的国家。这个国家有一条非常奇葩的规定，他们要求来到这里的旅行者必须说明他们来这里要做什么，如果说错就要处以绞刑。不论旅行者说什么，都可能会遭到这个国家的阻挠，导致他做不成，最终以绞刑告终。

但是，有一个旅行者非常聪明。在被问到这个问题的时候，他想了想说：我是来受绞刑的。这句话一说出来，连士兵也傻眼了。如果说这个人说对了，那么按照规定，他们是不可以给他处以绞刑的；但是，如果他说错了，那么他来到这里就不是受绞刑的，那么就更没有理由绞死他了。就这样，这个人保全了自己的性命。

3、理发师悖论

其实说起来，理发师悖论和说谎者悖论有点类似。这个悖论是说有一个理发师非常奇怪，他定下了一个很有意思的规定，那就是要给当地不为自己理发的人理发。这个规定就是一个悖论：他要不要给自己理发呢？

如果如果他不给自己理发，那么他就是当地不给自己理发的人，他就是自己应该理发的对象；如果他给自己理发了，那么他就打破了自己的规定，因为他不为那些能给自己理发的人理发。

4、忒修斯之船

忒修斯之船最早来自于公元1世纪的古希腊哲学家普鲁塔克，他提出了一个著名的思想实验：假设有一只大船，随着时间的推移在不断地老化，人们不得不持续地给它更换甲板、零件、设备。

最开始的时候，它只更换了一块甲板。随着时间的推移，更换的部分越来越多，直到某一天，连最后一块原始的甲板都已经被更换掉了。那么，这艘船还是原来的船吗？

如果说这艘特修斯之船是一艘新船，那么问题来了：这艘船从来没有消失过，何来新船一说呢？如果说它还是原来的那艘船，这也说不通，因为老船上所有的物件都不在了，凭什么说它还是当初那艘船呢？

5、电车难题

所有的悖论之中，没有一个比电车难题更加备受争议了，因为这里涉及到了伦理问题。这个悖论假设：有一辆火车（或者有轨电车）在轨道上行驶，突然发现有一个丧心病狂的人在前方轨道上绑了5个人。此时列车已经来不及刹车了，眼看着5个无辜的人危在旦夕。

这个时候，驾驶员发现轨道有一条岔路，可以紧急转弯。然而令人绝望的是，在那条岔路上，也有一个人被绑在了轨道上。那么，他该不该转向呢？

乍看之下，转向是一个比较好的选择，毕竟谁都知道5＞1的道理，这样可以多挽救四条性命。可是，岔路上的那个人难道就不是活生生的人命吗？他为何就要倒霉呢？而且，如果司机主动选择转弯，那么他就从一个原本无奈之人变成了一个主动的杀人犯，这样真的合适吗？